纯属降低复习效率^^
随机事件与概率
概率论引言————概率的意义
概率论:研究相继发生或者同时发生的大量随机现象的平均特性
概率论的目的:用事件的概率来描述和预测这些平均特性
事件A概率:P(A)
随机事件及其运算
确定概率数据P(A)的方法:频率方法,古典方法,几何方法,主观方法
样本点 ω:表示基本结果
样本空间 Ω={ω}:随机现象一切可能基本结果的集合
认识随机现象首先列出他的样本空间:
- 抛一枚硬币的样本空间 Ω = {ω1,ω2} #离散样本空间
- 电视机寿命的样本空间 Ω = {t: t≥0} #连续样本空间
随机事件:随机现象的某些样本点组成的集合(子集),用A,B,C等表示
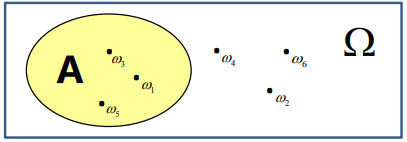
随机事件关系:
- 包含关系
- 相等关系
- 互不相容
随机事件运算:并集(或),交集(与),差集,补集(非)
运算律:交换律,结合律,分配律,对偶律
要求:一些对偶律的证明
概率定义及性质
概率:随机事件发生的可能性大小
公理化定义:对样本空间认一事件A,P(A)满足非负性、规范性(归一化)、可列可加性,则称P(A)是事件A的概率
频率方法:用频率稳定值获得概率
古典方法:经验事实基础上,对事件可能性进行逻辑分析获得该概率(事件所含样本点占所有样本点的比重 K/N)
要求:排列组合运用
几何方法:作图求事件区域占总区域的比重获得概率
要求:线性规划运用
概率性质:
- 空集概率为0
- 有限可加性(互不相容事件概率可加)
- 逆事件概率(1-P)
- 差事件概率(包含关系则P(B-A)=P(B)-P(A))
- 任意事件概率加法公式
要求:运用概率性质将复杂事件简化
条件概率
条件概率:某事件发生条件下,另一事件的概率,记为P(A|B)
P(AB)≠P(A|B)
%E2%89%A0P(A|B).png)
定义:A,B两随机事件,P(B)>0,则称P(A|B)=P(AB)/P(B)为事件B发生条件下,A发生的条件概率
概率的乘法公式:
- 若P(B)>0,则 P(AB) = P(B)P(A|B)
- 若P(ABC)>0,则 P(ABCD)= P(A)P(B|A)P(C|AB)P(D|ABC)
全概率公式:设样本空间的一个分割,每一块概率都大于零,则任何事件的概率可以由分割的每一块的概率乘此基础上事件发生的条件概率再对分割求和得到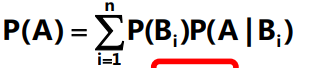
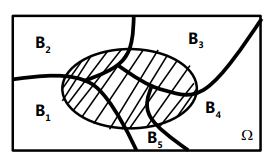
贝叶斯公式:后验概率公式
要求:全概率公式与贝叶斯公式熟练运用
事件的独立性
如果 P(AB)=P(A)P(B) 成立,则称事件A和B相互独立,简称A和B独立,否则称A和B不独立或相依。
要求:事件独立性判断
多事件独立性判断:
P(AB)=P(A)P(B),P(AC)=P(A)P(C),
P(BC)=P(B)P(C),P(ABC)=P(A)P(B)P(C)
最后一个条件说明:多事件两两独立不一定相互独立
随机变量及其分布
随机变量及其分布
随机变量:用来表示随机现象结果的变量
定义:
定义在样本空间Ω上的实值函数X=X(Ω)称为随机变量
随机变量仅可能取有限个或可列值,定义其为离散随机变量
随机变量的可能取值充满数轴上的一个区间(a,b),定义其为连续随机变量,a可为-∞,b可为+∞
分布函数F(x)=P(X≤x)
分布函数性质:单调性(单调非减),有界性,右连续性
离散随机变量概率分布列:p(xi)=P(X=xi)
性质:非负性,正则性
连续随机变量概率密度函数:p(x)=F’(x)
性质:非负性,正则性,若干点上值的不同不影响积分值
要求:
已知密度函数求概率
已知分布函数求密度函数
已知密度函数求分布函数
随机变量的数学期望
离散随机变量数学期望: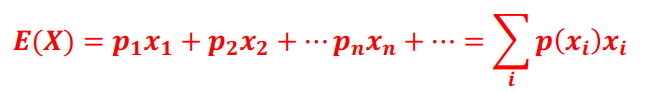
连续随机变量数学期望: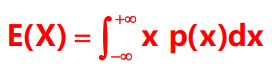
定理:X的函数的数学期望可以用X的分布来计算
要求:
微积分基础
级数基础
熟练期望性质简化计算
随机变量的方差与标准差
方差: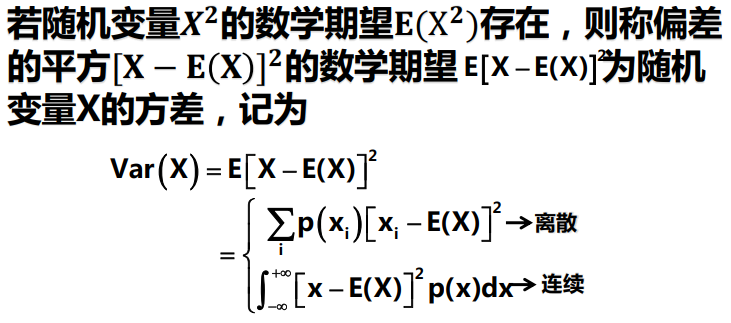
标准差:
方差性质:
- $$Var(X)=E(X^2)-E^2(X)$$
- 常数方差为0
- $$Var(aX+b)=a^2Var(X)$$
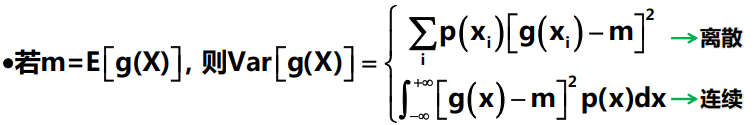
切比雪夫不等式:
要求:
熟练运用方差的性质简化计算
掌握切比雪夫不等式
常用离散分布
二项分布:
$X\sim b(n,p)$
$$ P(X=k)=C^k_np^k(1-q)^{n-k}$$
$$E(X)=np$$
$$Var(X)=np(1-p)$$
泊松分布:
$X\sim P(λ)$
$$P(X=k)=\frac{λ^k}{k!}e^{-λ}$$
$$E(X)=λ$$
$$E(X^2)=λ^2+λ$$
$$Var(X)=λ$$
要求:熟练掌握常用离散分布二级公式
常用连续分布
正态分布
$X\sim N(μ,σ^2)$
$$p(x)=\frac{1}{\sqrt{2\pi}σ}e^{-\frac{(x-\mu)^2}{2\sigma^2}} ,-\infty<x<\infty$$
$$E(X)=\mu$$
$$Var(X)=\sigma^2$$
正态变量的标准化:
$$P(X\leqslant c)=\Phi(\frac{c-\mu}{\sigma})$$
延伸: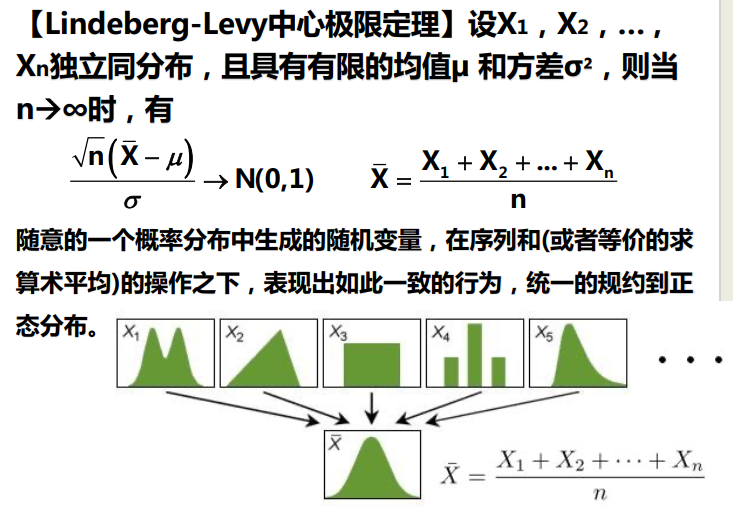
均匀分布
$X \sim U(a,b)$
$$
p(x)=\begin{cases}
\frac{1}{b-a} & {a<x<b} \\
0 & {else}
\end{cases}
$$
$$E(X)=\frac{a+b}{2}$$
$$E(X^2)=\frac{a^2+ab+b^2}{3}$$
$$Var(X)=\frac{(b-a)^2}{12}$$
指数分布
$X\sim Exp(λ),λ>0$
$$ p(x)=\begin{cases}
λe^{-λx} & {x\geqslant0} \\
0 & {x\leqslant0}
\end{cases}
$$
$$E(X)=\frac{1}{λ}$$
$$E(X^2)=\frac{2}{λ^2}$$
$$Var(X)=\frac{1}{λ^2}$$
$$(捷径)P(X>s)=e^{-λs}$$
要求:
熟练掌握各连续分布二级公式
重点熟悉正态分布
随机变量函数的分布
离散随机变量函数的分布
1.列出X的分布列
2.将分布列X换成Y=g(X)
3.将分布列Y相等的项合并,对应概率相加
连续随机变量函数的分布
一般方法
- 求Y的分布函数$F_Y(y)$
$$F_Y(y)\to P(Y \leqslant y)=P(g(X) \leqslant y)=P(X \in {x|g(X)\leqslant y})$$
2.对$F_Y(y)$求导,得到$f_Y(y)$
$$f_Y(y)=F’_Y(y)$$
定理:若随机变量X的密度函数为$p_X(x)$ ,随机变量Y=g(X)为另一随机变量,当 g(x) 是严格单调函数,其反函数h(y)有连续导函数,则随机变量Y=g(X)的密度函数
$$
p_Y(y)=
\begin{cases}
p_X[h(y)]|h’(y)| & {a<y<b}\\
0 & {else}
\end{cases}
$$
$$a=min\lbrace{g(-\infty),g(+\infty)}\rbrace,b=max\lbrace{g(-\infty),g(+\infty)}\rbrace$$
定理:正态分布的线性函数仍服从正态分布
定理: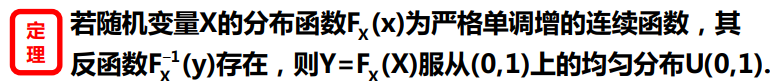
分布的K阶矩
如果以下数学期望存在,则称:
$\mu_k=E(X^k)$ 为X的k阶原点矩
$v_k=E^k(X-E(X))$ 为X的k阶中心矩
多维随机变量及其分布
多维随机变量及其联合分布
多维随机变量的研究思路:
- 离散随机变量:联合分布列
- 连续随机变量:联合密度函数
定义:$X(\omega_1),X(\omega_2)…X(\omega_n)$是定义在同一个样本空间上的n个随机变量,则称$X(\omega)=(X(\omega_1),X(\omega_2)…X(\omega_n))$为n维随机变量或随机向量
联合分布函数:$F(x_1,x_2,…,x_n)=P(X_1<x_1,X_2<x_2,…,X_n<x_n)$
联合分布函数性质:
- 单调性
- 非负性+有界性
- 右连续性
tip:概率论部分主要讨论二维随机变量
二维离散型随机变量的联合分布列: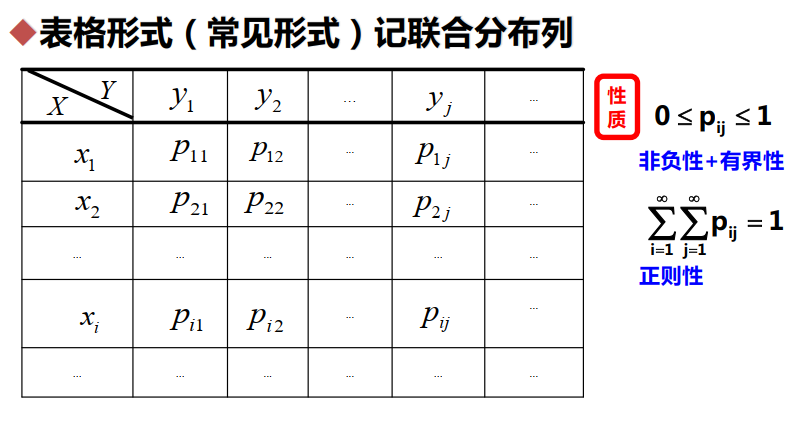
二维连续型随机变量的联合概率密度:

常用多维分布
多项分布

二维均匀分布

二维正态分布

边际分布与随机变量的独立性
引言
二维联合分布函数含有“丰富的信息”:
- 每个分量的分布——边际分布
- 两个分量之间的关联程度——协方差、相关系数
- 给定一个分量时,另一个分量的分布——条件分布
边际分布函数

边际分布列

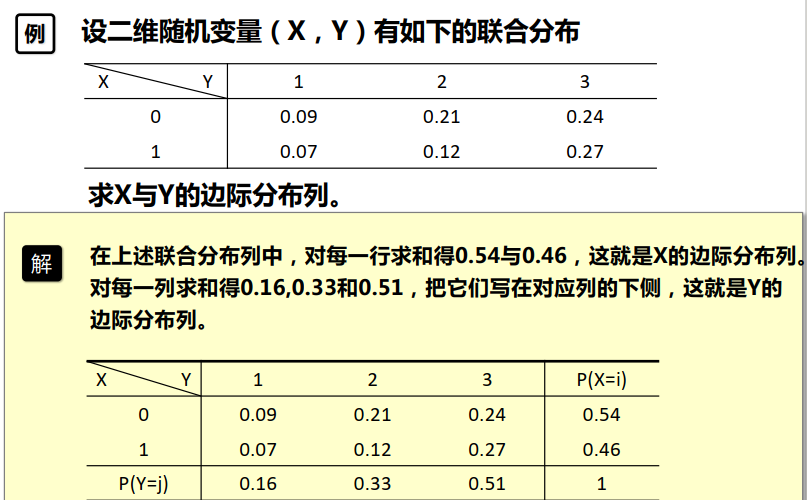
边际概率密度
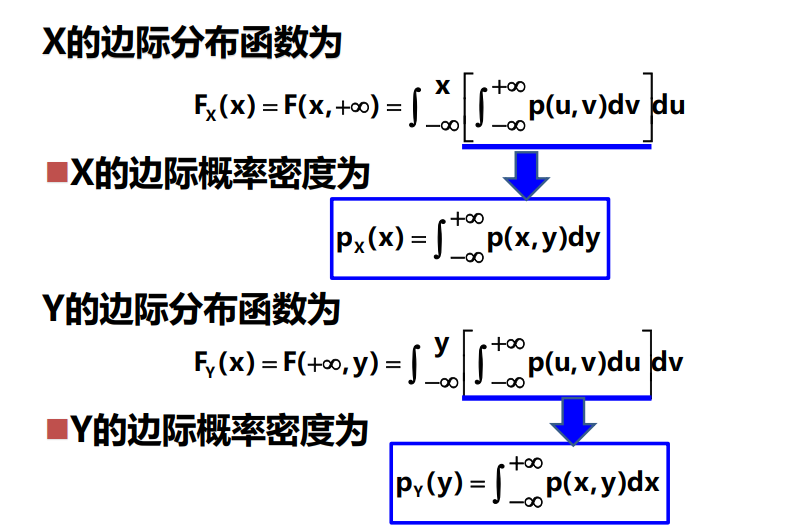
二维正态分布的边际分布

随机变量间的独立性

多维随机变量函数的分布
设(X,Y)是二维随机变量,其联合分布函数为F(X,Y),Z=g(X,Y)是随机变量X,Y的二维函数。Z的分布函数:
$$F_Z(z)=P(Z<z)=P(g(x,y)<z)$$
两个独立随机变量的和的分布
连续场合的卷积公式

离散场合的卷积公式
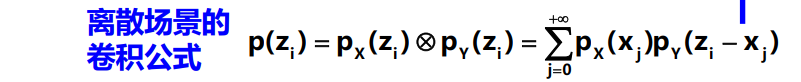
正态分布可加性
随机变量$X \sim N(\mu_1,\sigma_1^2),Y \sim N(\mu_2,\sigma_2^2)$,且X与Y独立,则:
$$Z=X+Y \sim N(\mu_1+\mu_2,\sigma_1^2+\sigma_2^2)$$
泊松分布可加性
$$Z=X+Y \sim P(\lambda_1+\lambda_2)$$
二项分布可加性
$$Z=X+Y \sim b(n+m,p)$$
例:最大值分布


例:最小值分布


要求:
熟练掌握随机变量函数
学会分析题意灵活解题(多刷题)
多维随机变量的特征数
数学期望

方差

数学期望和方差的运算性质
任何时候都成立:
$E(X+Y)=E(X)+E(Y)$
随机变量独立时成立:
$E(XY)=E(X)E(Y)$
$Var(X+Y)=Var(X)+Var(Y)$

协方差
描述两个随机变量的相互关系信息
定义:
$Cov(X,Y)=E[(X-E(X))(Y-E(Y))]$
$Cov(X,X)=Var(X)$
性质:
$Cov(X,Y)=E(XY)-E(X)E(Y)$(常用)
$Cov(X,Y)=0$ (X,Y相互独立)
$Var(X±Y)=Var(X)+Var(Y)±2Cov(X,Y)$
$Cov(X,Y)=Cov(Y,X)$
$Cov(X,a)=0 (a为常数)$
$Cov(aX,bY)=abCov(X,Y)$
$Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z)$
相关系数
协方差带有量纲,为了消除量纲的影响,引入相关系数这一无量纲的量

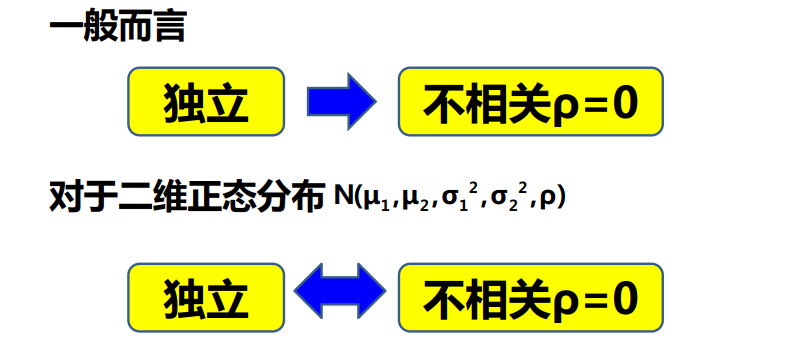
性质:
$[Corr(X,Y)]^2 \leqslant 1$
$Corr(X,Y)=±1$的虫咬条件是存在a(≠0)与b,使得
$$P(Y=aX+b)=1$$
其中,
$Corr(X,Y)=1$时,a>0
$Corr(X,Y)=-1$时,a<0

随机向量的数学期望与协方差矩阵

条件分布与条件期望
条件概率
$$P(A|B)=\frac{P(AB)}{P(B)}$$
全概率公式
$$P(A)=\sum_{i=1}^n P(B_i)P(A|B_i)$$
贝叶斯公式
$$P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_{j=1}^n P(B_j)P(A|B_j)}$$
离散随机变量的条件分布
$$p_{i|j}=P(X=x_i|Y=y_j )=\frac{P(X=x_i,Y=y_j )}{P(Y=y_j )}=\frac{p_{ij}}{p_{gj}}$$
$$F(y|x_i)=\sum_{y_j<y}P{Y=y_j|X=x_i}=\sum_{y_j<y}p_{j|i}$$
连续随机变量的条件分布
$$p(x|y)=\frac{p(x,y)}{p_Y(y)}$$
$$F(x|y)=P(X \leqslant x|Y=y)=\int_{-\infty}^x\frac{p(u,y)}{p_Y(y)}du$$
连续场合全概率公式

连续场合贝叶斯公式
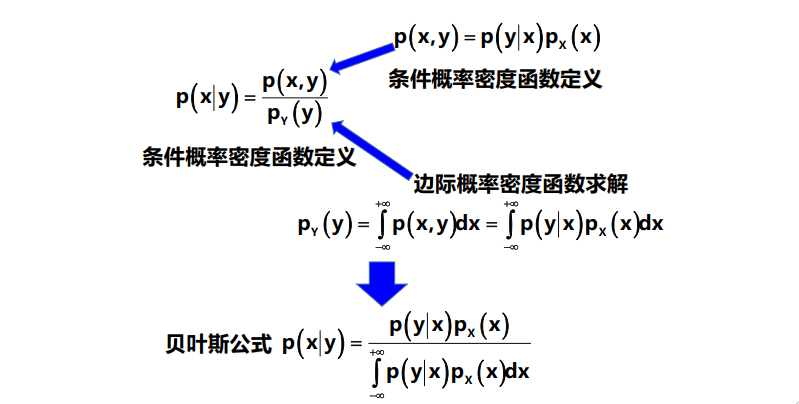
条件数学期望

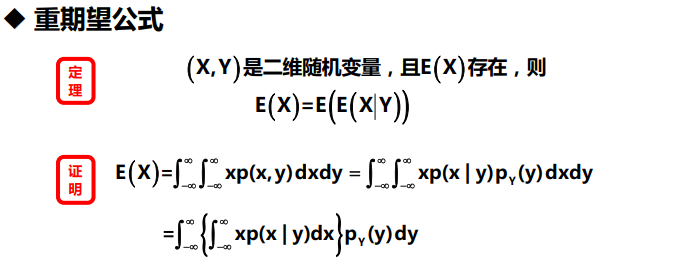


大数定理和中心极限定理
随机变量序列的两种收敛性
依概率收敛(强收敛)

按分布收敛(弱收敛)

例:两种收敛不等价

大数定理
大数定理概述

切比雪夫不等式

应用范围:分布未知,知道期望与方差
辛钦大数定理(样本平均数稳定性定理)

伯努利大数定理(频率稳定性定理)

中心极限定理
概述

独立同分布的中心极限定理
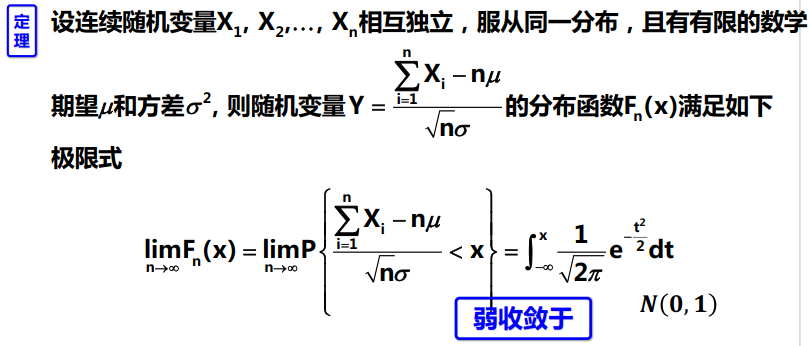

棣莫弗—拉普拉斯中心极限定理(二项分布弱收敛于正态分布?)

独立不同分布的中心极限定理
林德伯格中心极限定理(感觉不太实用的一个)

李雅普诺夫中心极限定理


